텐서를 충분히 이해하기 위해서는 실수, 복소수, 스칼라, n차원의 벡터. 벡터의 계산, 행렬, 베이시스, 미분법, 데카르트 좌표계, 원통 좌표계, 구 좌표계, 기초 다이애드곱(텐서곱)의 개념이 필요한데 이것들을 다 설명하는 것은 불가능하다는 결론을 내렸습니다.
따라서 텐서라는 추상적인 개념을 최대한 쉬운 개념에 대한 설명을 해보려고 합니다.
기초. 스칼라와 벡터, 벡터의 표기법
스칼라는 크기만 나타내는 값이고 벡터는 크기+작용점+방향이 있는 값입니다.
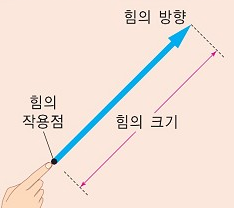
fig 1. 벡터
이제 벡터를 좌표계로 가져간다고 생각해봅시다.
벡터를 좌표계로 가져간다면 위의 작용점을 원점에 놓고 x좌표와 y좌표를 이용하여 벡터의 크기와 방향을 보여줄 수 있게 됩니다.
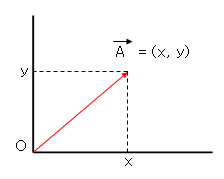
fig 2. 2차 좌표평면계에서 벡터의 표현
2차 좌표 평면계에서 벡터는 '(벡터이름)=(x,y)' 이렇게 표시합니다. 벡터의 특징은 벡터이름 위에 화살표를 표기하여 벡터임을 알려줍니다.
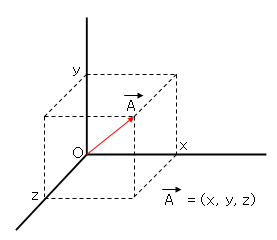
fig 3. 3차 좌표평면계에서 벡터의 표현
3차원으로 옮겨오더라도 2차원의 특성과 동일하다는 것을 알 수 있습니다. 2차원과 다른 점은 z라는 요소가 하나 추가되었다는 점입니다.
여기서 표기법을 행렬로 바라봅시다. 행렬 개념을 적용하면 위의 2차원 벡터 표기법은 1X2행렬이라고 볼 수 있고 3차원의 경우 1X3으로 볼 수 있습니다. 여기에 전치행렬 개념을 적용시킨다면 1X2 -> 2X1, 1X3 -> 3X1 로 바꿀 수 있습니다.
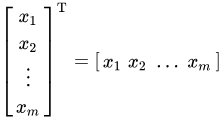
fig 4. 전치행렬 개념의 적용
이런 방법으로 우리가 익숙하게 접해왔던 좌표 평면계에서 위치 표기법을 행렬의 개념에서 바라볼 수 있게 되어야 합니다.
본론. 텐서란 무엇인가?
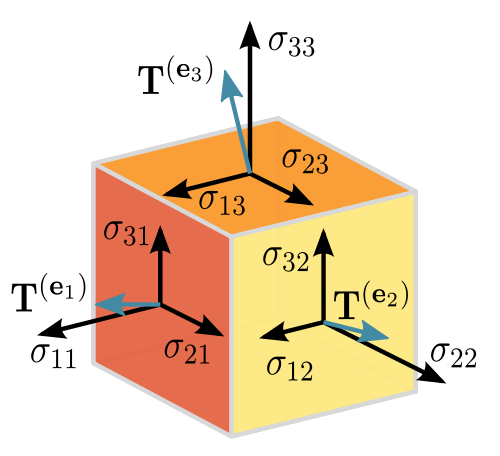
fig 5. 텐서
텐서란 벡터보다 넓은 개념으로 임의의 기하 구조를 좌표 독립적으로 표현하기 위한 표기법입니다.
이는 벡터의 필수 요소인 '작용점'에서 벗어나서 그 자체만으로 절대적인 벡터적 의미를 가지기 위해 사용되는 개념입니다.
예를 들어 위의 3차원 벡터를 보면 데카르트 좌표계, 원통 좌표계, 구 좌표계 등의 여러 좌표계에서 봤을 때 모두 다른 값을 가집니다. 이는 좌표계의 특성상 무엇을 표현할 것인가가 서로 다르기 때문에 발생하는 문제입니다.
[데카르트 좌표계는 3개의 스칼라값(우리에게 익숙한 (3,2,1)의 개념), 원통 좌표계는 2개의 스칼라값과 1개의 각도값, 구 좌표계는 1개의 스칼라값과 2개의 각도값을 가집니다.]
이러한 좌표계 변화에 따른 벡터값의 변화와 무관하게 3가지 다른 값은 모두 동일한 벡터를 가르킵니다. 이것이 텐서의 개념입니다. 벡터가 가지는 본질을 표현하는 것이 텐서입니다. 이런 설명을 본다면 텐서가 벡터보다 더 좁은 개념이라고 생각할수도 있습니다. 하지만 반대입니다. 텐서는 벡터보다 확장된 개념입니다. 그 이유는 벡터는 단 한 개의 값을 담을 수 있지만 텐서는 여러 벡터의 값을 자기 자신에 담을 수 있기 때문입니다.
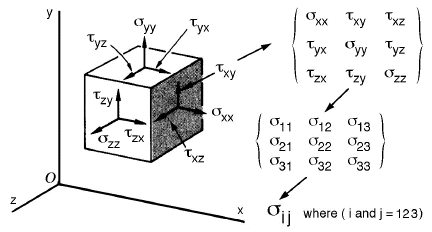
fig 6. 텐서의 예시
텐서는 내부에 많은 벡터(정보)를 담을 수 있는 구조체라고 인식한다면 훨씬 이해가 쉬울 것입니다. 이는 데이터 프레임인 컨테이너나 컬렉션의 개념과도 비슷합니다.
텐서 플로우를 이해하는데 있어 가장 중요한 텐서의 개념은
1. 상대적이지 않고 절대적인 값
2. 많은 정보를 담을 수 있다.
입니다.
ref.
wikipedia / tensor / fig 5
- https://en.wikipedia.org/wiki/Tensor
University of Cambridge / What is tensor?
-https://www.doitpoms.ac.uk/tlplib/tensors/what_is_tensor.php
조금은 느리게 살자 / 텐서(tensor)
-https://ghebook.blogspot.kr/2011/06/tensor.html
Weistern's / dyad
-http://sciphy.tistory.com/616
JavaLab / 힘의 합력(벡터 합성) / fig 1
-http://javalab.org/lee/2015/addition_of_force/
Nick Lib / 인공지능에 자주 나오는 수학 2 - 벡터 공간과 벡터 내적 / fig 2, fig 3
-http://bbs.nicklib.com/algorithm/1670
위키백과 / 벡터 행렬 / fig 4
-https://ko.wikipedia.org/wiki/%EB%B2%A1%ED%84%B0_%ED%96%89%EB%A0%AC
Quora / Is stress is a tensor? / fig 6
-https://www.quora.com/Is-stress-is-a-tensor
'데이터 분석 > 데이터 분석 기초 자료' 카테고리의 다른 글
| 데이터 마이닝의 종류 (0) | 2018.04.16 |
|---|---|
| 텐서플로우(TensorFlow)를 사용하기 위한 플로우(Flow)에 대한 설명 (0) | 2018.04.15 |
| rJava를 이용한 Java R 연동하기 (비추천) (0) | 2018.04.13 |
| Rsession을 이용한 R출력 (추천) (0) | 2018.04.11 |
| Rserve를 이용하여 jsp웹에 그래프 출력하기 (0) | 2018.04.10 |